Context
The application of compressed sensing techniques to US imaging has motivated research efforts only recently, since the first works were published in 2010 and therefore few studies have been devoted to this topic to date. A key element in CS is that the data to be reconstructed should have a sparse expansion in some basis or dictionary. Another important feature for ensuring a successful CS reconstruction is the way the measurement of the data is performed. We proposed a new approach based on the use of learned overcomplete dictionaries that allow for much sparser representations of the signals since they are optimized for a particular class of images such as US images.
Method
Our objective was to investigate in details the feasibility of compressive sensing 3D ultrasound. The results
- First, we addressed CS reconstruction of 3D US images using learned overcomplete dictionaries. We showed in particular that the learned dictionary approach yields better performances than conventional sparsifying dictionaries based on fixed transforms such as Fourier or discrete cosine.
- Secondly, we evaluated the generality of the learned dictionary approach. Indeed this approach may be hampered by overlearning, yielding a learned dictionary providing satisfying reconstruction only for images very close to the learning set. We showed that it is possible to build a dictionary allowing to reliably reconstruct different volumes of different ex vivo and in vivo organs.
- Thirdly, we focused on the line-wise sampling of entire RF lines which results in an increase of the frame rate since we work on the reconstruction of the envelope image. We study the influence of the sampling strategy on simulated data, by comparing in each case the 2 most common sampling patterns, i.e. point-wise and line-wise random patterns. We showed in particular that although not fully uniform, the line-wise sampling results in an accuracy comparable to the conventional point-wise sampling, using the dictionary based strategy we propose. This indicates that CS acquisition of 3D data is feasible in practice in a relatively simple setting.
We have chosen the K-SVD algorithm to learn the overcomplete dictionary due to its efficiency and ease of implementation.
The sampling protocols in US imaging have to be designed to fulfill both the requirements of CS and of the US devices. As a result, two main sampling strategies are then possible: point-wise random sampling, which corresponds to the standard CS settings, or line-wise sampling, which has the advantage of yielding a simple practical implementation for ultrasound acquisitions.
We tested three representation bases, namely Fourier, DCT and the dictionary learned using the K-SVD method.
 | Figure 1: Sampling masks R1 and R2 adapted to a spatial sampling of 3D US volumes. The black pixels correspond to the samples used for CS. The proportion of samples here is of 50% of the original volume. |
Results
We have tested the feasibility on simulated and experimental data which have been presented in [3].
Simulation data reconstruction results
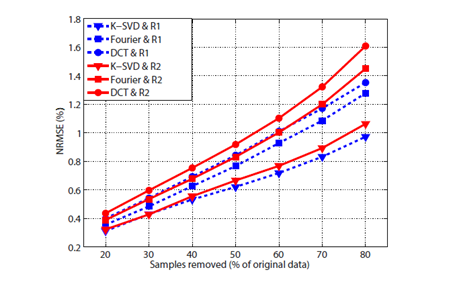 | Figure 2: NRMSE as a function of the number of samples removed using the sampling masks R1 and R2. The error is computed on the envelope of the 3D US volumes after CS reconstruction using K-SVD dictionary, Fourier basis and DCT. |
 | Figure 3: Visualization of 3D CS reconstructions of a simulated US volume using the sampling mask R2 in Cartesian coordinates. Original data, Fourier based reconstruction using a 50% subsampling rate, K-SVD based reconstruction using a 50% subsampling rate, Fourier based reconstruction using a 80% subsampling rate and K-SVD based reconstruction using a 80% subsampling rate. |
Experimental data reconstruction results
Ex vivo experimental results
 |
| Figure 4: Visualization of 3D CS reconstructions of an ex vivo kidney US volume using the sampling mask R2 Cartesian coordinates. Reconstructions using the K-SVD dictionary for 50 and 80% subsampling rates. |
In vivo experimental results
 |
| Figure 5: Visualization of 3D CS reconstructions of an in vivo liver US volume using the sampling mask R2. Reconstructions using the K-SVD dictionary for 50 and 80% subsampling rates. |
