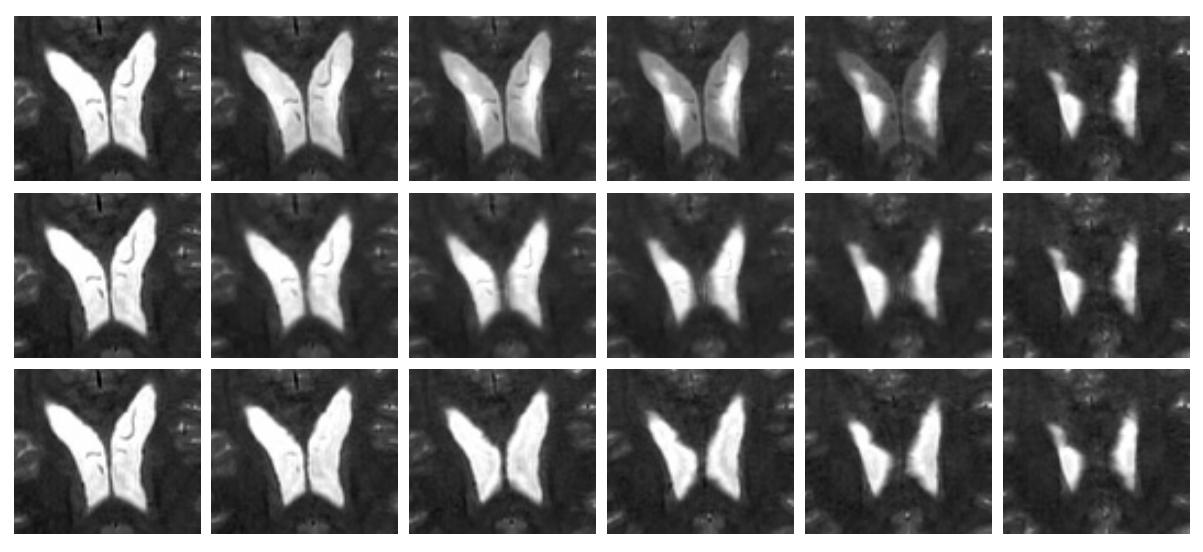
Invertibility in image registration is usually enforced using the flow of diffeomorphism approach: the transformation is the solution at t=1 of the nonlinear transport equation. This approach prevent the use of a parametric model to model the transformation. Consequently, when using B-Spline transform, soft or hard constraints on the transformation Jacobian are usually imposed during the registration to penalize non invertible transform as in [1]. Our goal is to find constraints on the B-Spline coefficients to guarantee that the transformation is a diffeomorphism. The main result obtained in [2] is that B-Spline vector field are diffeomorphic when discrete Jacobians of the B-spline coefficients are positive. A diffeomorphic B-spline registration algorithm has been proposed. A comparison with state of the state is presented on the famous disk to C registration problem (our method is at the bottom right): This algorithm has been used for interslice interpolation. Below is the results of an interpolation between two slices. Linear interpolation is on the top line, our results in the middle and the ground truth is on the bottom line:

References