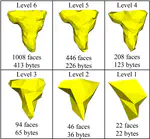
This work aims at computing multiresolution analysis on 3D triangular meshes
Method
Based on the inversion of an irregular subdivision scheme1, our algorithm is able to construct a complete hierarchy of meshes from one original mesh2. This simplification is reversible, and the information to reconstruct the original mesh connectivity from the lowest resolution mesh is a compact code, well suited for connectivity compression. The subdivision paradigm allows our approach to apply the wavelet decomposition on the mesh geometry (the vertices coordinates), the filter bank being constructed by applying the lifting scheme on the “lazy” wavelets filter bank. Using this wavelet scheme, two compression approaches were proposed : compression with progressive resolution 3 or compression with progressive precision 4.
Source code and executable
Source code is available on github. This code is distributed under the GPL license. © CNRS, INSA-Lyon, UCBL, INSERM.