A. Gelas, O. Bernard, D. Friboulet and R. Prost
Purpose and context
The partial differential equation (PDE) driving level set evolution in segmentation is usually solved using finite differences schemes. We propose an alternative scheme based on radial basis functions (RBFs) collocation.
Methods
Substituting the RBF based implicit function whose zero level is the interface of interest into the PDE results in an Ordinary Differential Equation (ODE). We show that compactly supported RBFs (CSRBFs) are particularly well-suited to collocation in the framework of segmentation. CSRBFs allow reducing the computation cost using a Kd-tree based strategy for neighbourhood’s representation. We show that the usual reinitialisation step of the level set may be avoided by simply constraining the L1-norm of the CSRBF parameters. In addition this approach provides a continuous representation of both the implicit function and its zero level set
Experimental results
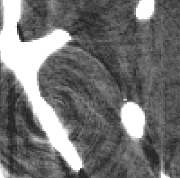 | 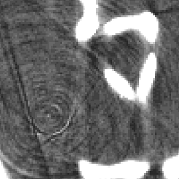 | 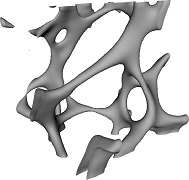 |
| Two slices of the original CT data of the calcaneus bone | segmentation of the image | |

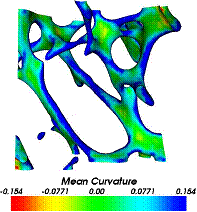
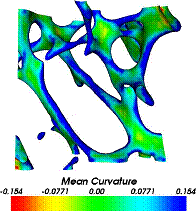
Distribution of the Gaussian and mean curvature over the surface of the segmented image References