SPECTRAL CT
Overview
Exploiting X-ray measurements acquired at multiple energies, spectral CT has the ability to recover the concentration maps of the constituents of the tissues in a quantitative manner. While the principle of dual-energy CT has been known for more than 30 years, recent developments in energy selective photon counting detectors have boosted the research in this area.
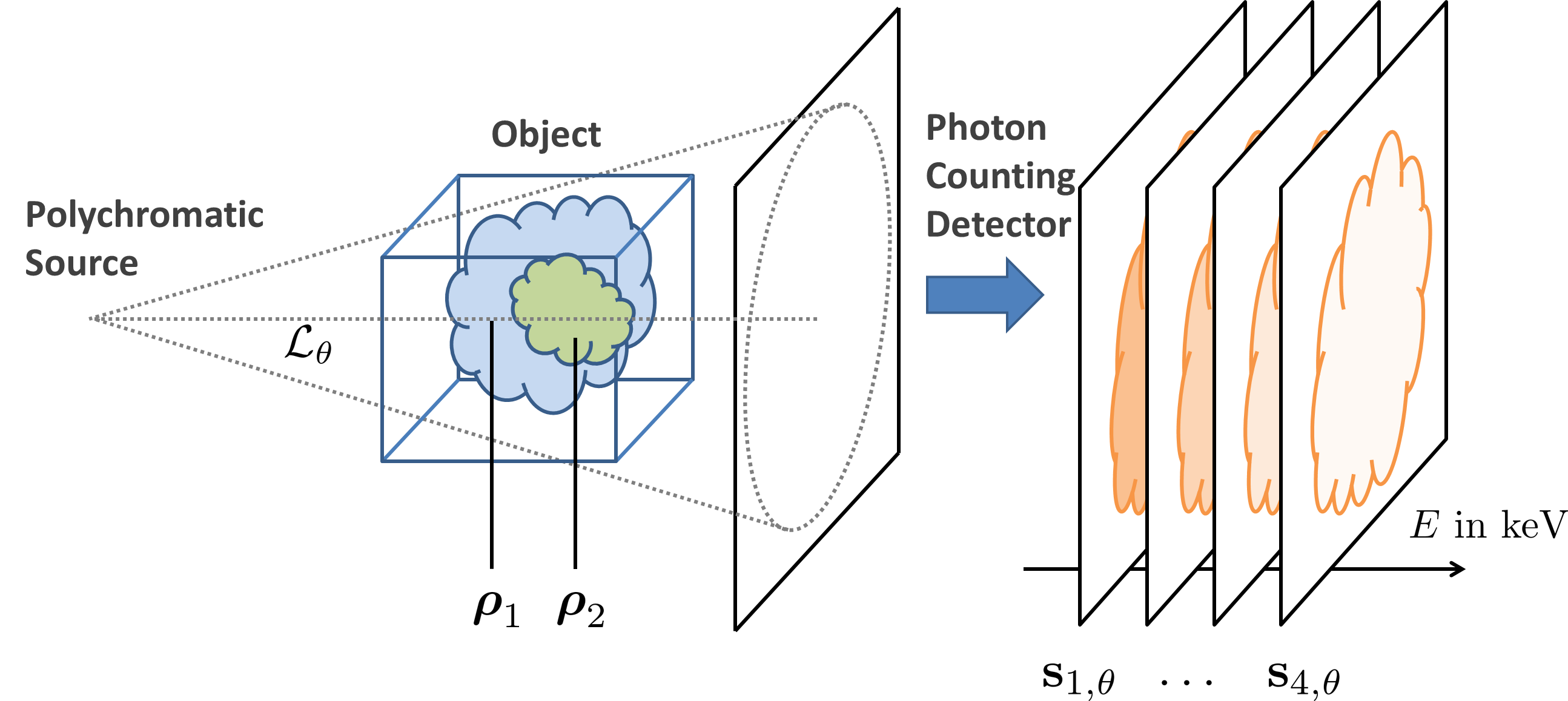
FIG. Principle of spectral CT acquisition
We consider an object made of $M$ materials, each with a density $\boldsymbol{\rho}_m$, which is imaged by a photon counting detector having $I$ energy bins. At each projection angle $\theta$, the photon counting detector provides $I$ projection images $\mathbf{s}_{i,\theta}$. Repeating the acquisition for $\Theta$ projections angles, we have
.$\mathbf{s} = \mathcal{G}(\boldsymbol{\rho})\quad$ with $\quad \begin{cases} \mathbf{s} = \{\mathbf{s}_{i,\theta}\}_{1 \le i \le I,\; 1 \le \theta \le \Theta}\\ \boldsymbol{\rho} = \{\boldsymbol{\rho}_m\}_{1 \le m \le M} \end{cases}$
where $\mathcal{G}$ denotes the (nonlinear) forward model that takes into account the acquisition geometry and detector response function.
The spectral CT problem consists in recovering the material density $\boldsymbol{\rho}$ from the energy-resolved projection images $\mathbf{s}$.
Regularization of Nonlinear Decomposition of Spectral X-ray Projection Images
We have introduced material-dependent regularization of projection images and proposed to solve the material decomposition problem using a Gauss-Newton algorithm that can benefit from fast linear solvers. Our method has been compared to the reference maximum likelihood Nelder-Mead algorithm and a 70x faster decomposition was obtained.
Download our toolbox and test our Matlab implementation!
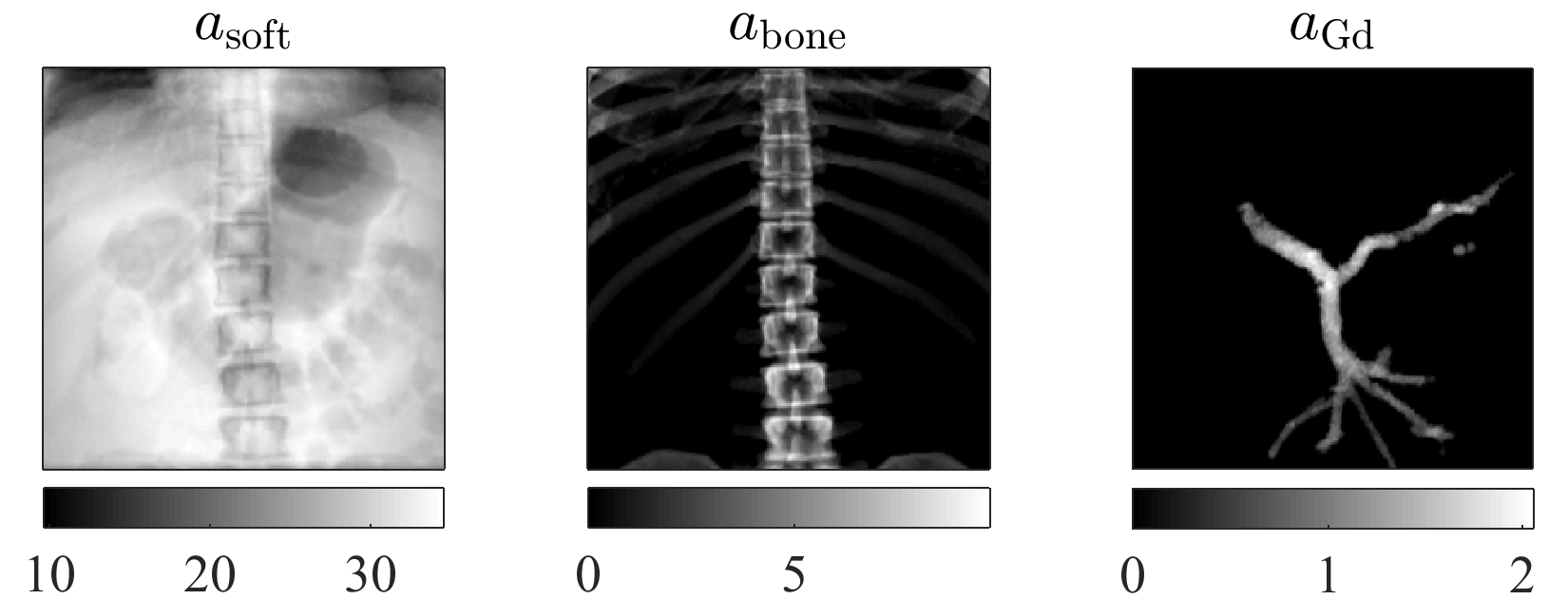
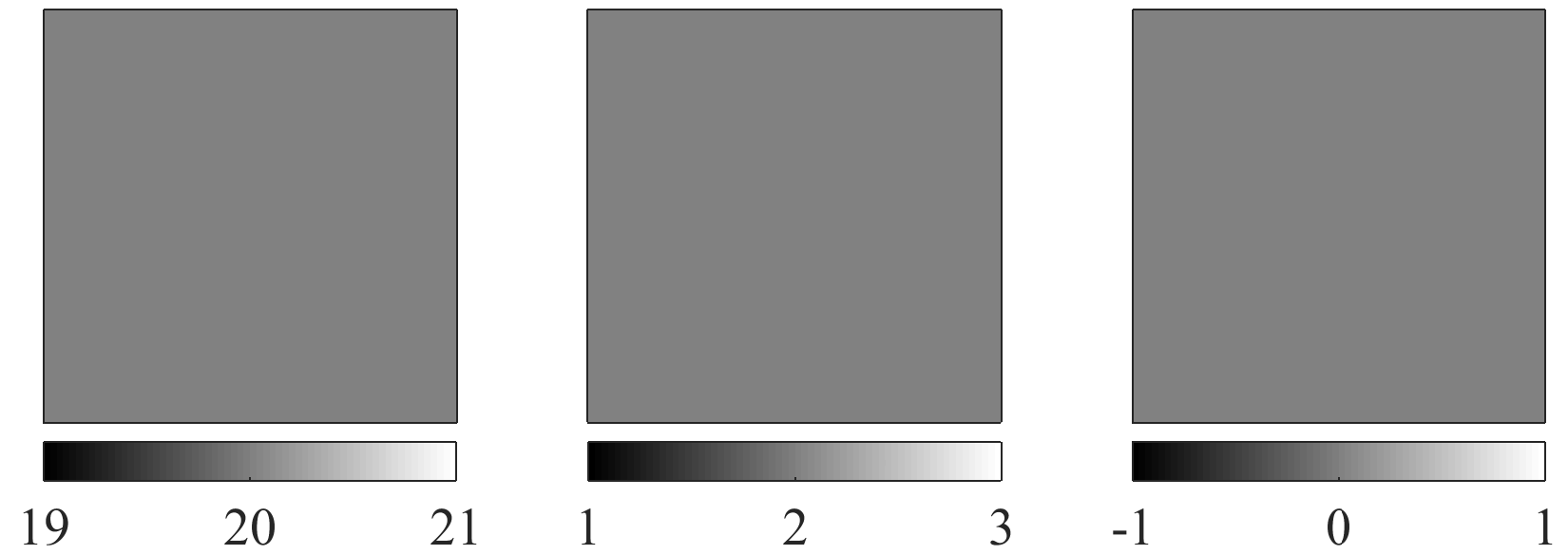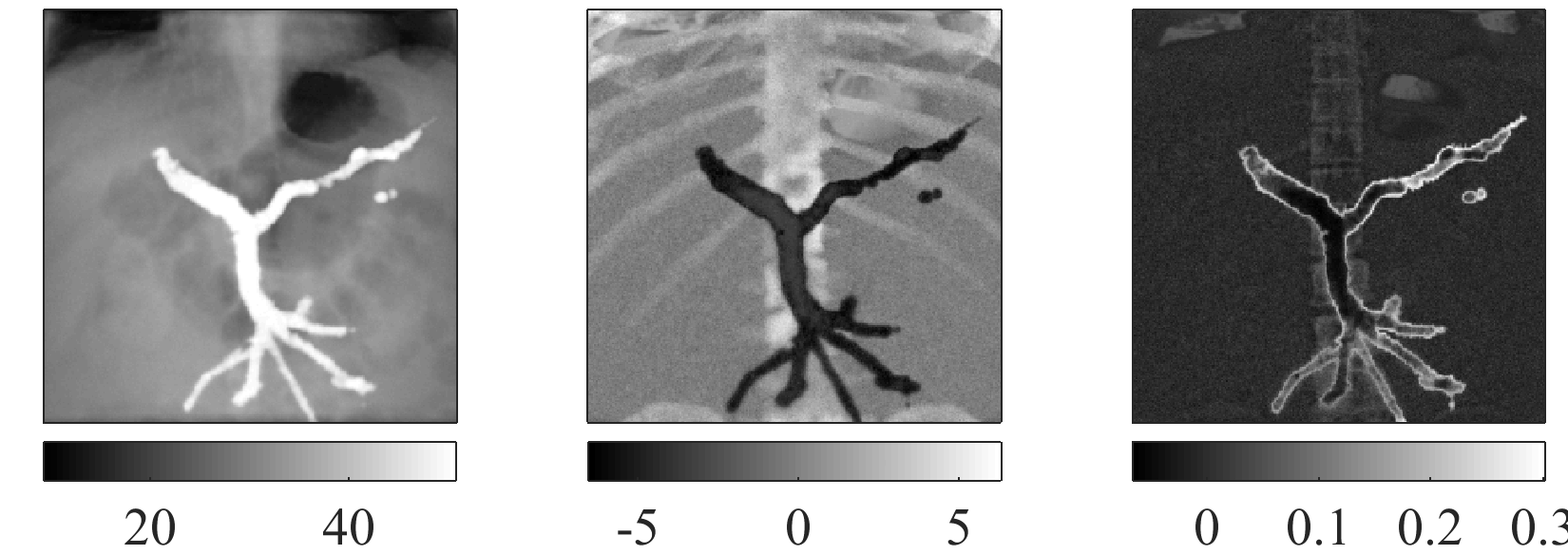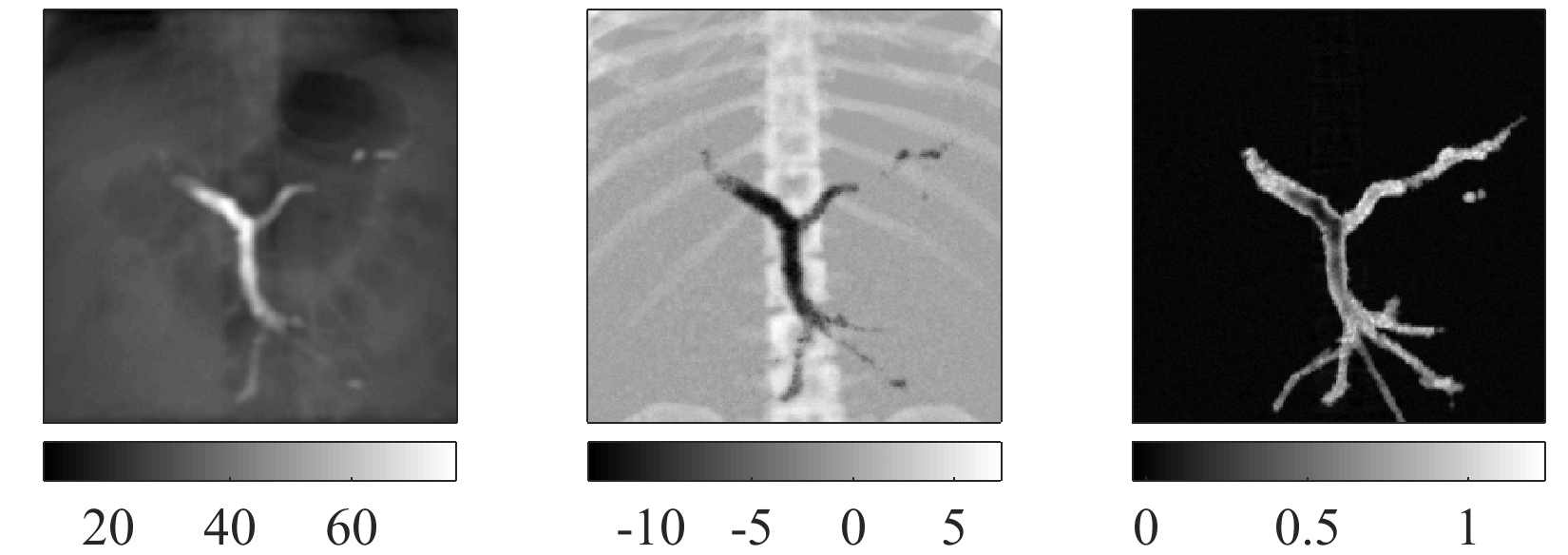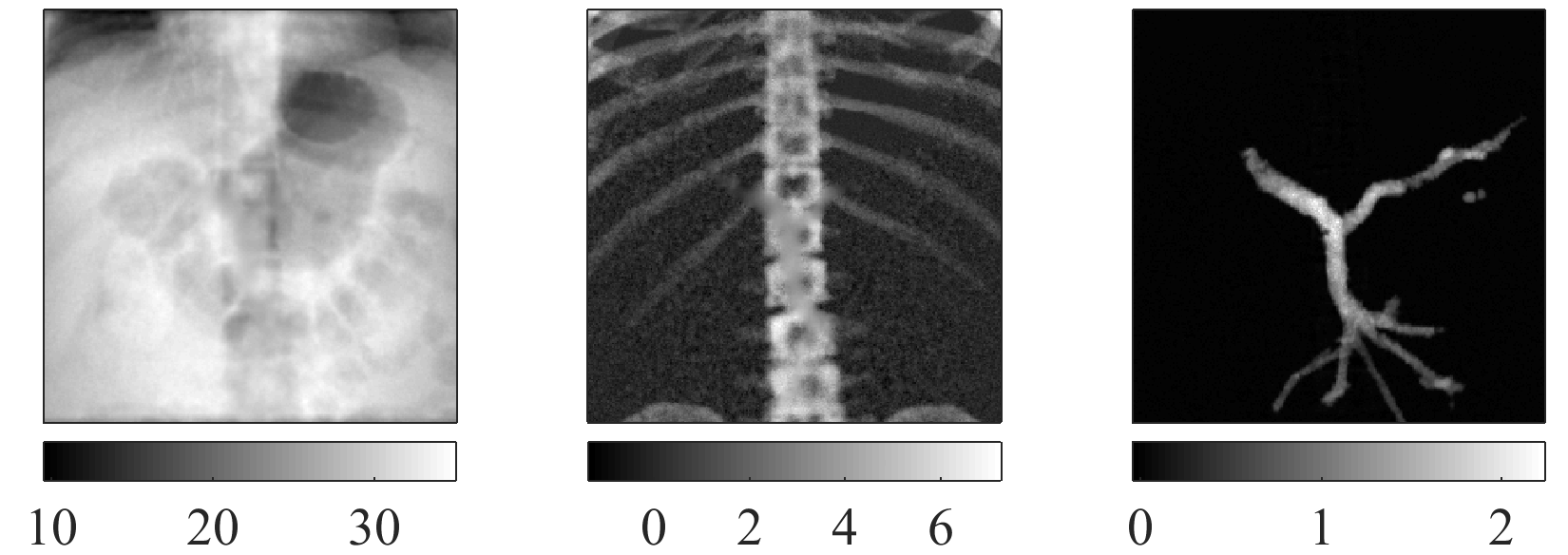
FIG. Our iterative decomposition algorithm in action in a thorax phantom. Top row: ground-truth material images. Bottom row: decomposed material images.
Citation: N. Ducros, J.F.P.J. Abascal, B. Sixou, S. Rit, and F. Peyrin, Regularization of Nonlinear Decomposition of Spectral X-ray Projection Images, Medical Physics, 44(9), e174-e187, 2017.